Fundamentals of Trigonometry: 1

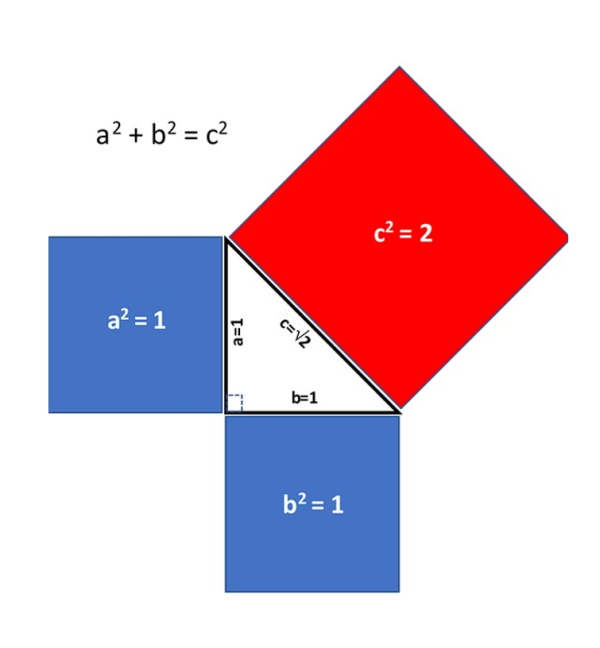
Pythagoras and irrational numbers: For any right-angled triangle where c is the hypotenuse and a and b are the other two sides then a2 + b2 = c2.

A right-angled triangle’s shape is orthogonal.
Two sides are square and one is diogonal (?)
Diagonal I mean — the hypotenuse.
Two angles are ‘cute and none is obtuse.
The right angle’s measure is 90 degrees.
That’s so even when it is isosceles.

The right angle’s big and it faces the long side.
The long side, remember? —  the hypotenuse.
Adjacent and opposite short sides aren’t wrong sides,
It’s just their names change with the angle you choose.
Arranging the terms with the short sides on one side,
The long and the short of it’s neatly construed:
Taking squares, then the short sides add up to the long side!               a² + b² = c²  

It’s as simple as that, and Pythagoras knew.

But notice: the long side, if short sides are 1 sized,                                     1² + 1² = c²                      
Is wildly irrational — the square root of 2.                                                   √2 = c           

Pythagoreans, in shock, became tongue-tied,
Their secret unspeakably wrong and yet true.

Joe Crocker

Pythagoras was so pleased when he discovered this relationship that he sacrificed an ox. Sadly, the Pythagoreans also believed that any real length could be expressed as the ratio of 2 integers. When it was shown by Hippasus that a triangle with unit sides had a hypotenuse which defied any such expression (i.e. an irrational number, the square root of 2) Hippasus was drowned for his heresy and the Pythagorean school sworn to secrecy. Or so legend has it.

If you have any thoughts on this poem,  Joe Crocker  would be pleased to hear them.